① 맥스웰 방정식은 전계와 자계의 관계를 나타내는 방정식으로 전자파의 해석에 있어서 기본이
되는 방정식이다.

MKS 단위계로 맥스웰 방정식을  써보자.

② 맥스웰 방정식을 이용해서 자유공간에서 파동 방정식을 유도해보자.
자유공간은   을 의미한다.
 패러더이 법칙 으로부터 좌 우변에 curl을 취하여    벡터 항등식을
이용한다.

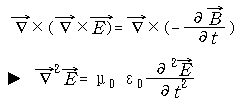
이것을 다시 쓰면 전계의 파동 방정식을 얻는다.

 는 전자기파의 속도임.

마찬가지 방법으로 다음의 자계의 파동 방정식을 얻는다.

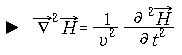
  이것이 의미하는 바는 전자기장는 파동방정식을 만족시키면서 진행하는 전자기파란 사실이다.

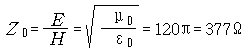
공간에서의 전계와 자계의 비는 공간의 저항 임피던스를 나타내는데, 를 매질의 특성 임피던스
(characteristic impedance), 파동 임피던스 (wave impedance) 또는 고유 임피던스 (intrinsic impedance)
라고 한다. 전계와 자계가 동일상일 때  는 순저항성이며, 이와같은 순저항성 매질은 자유공간과 무
손실 유전체 매질등을 의미한다.

③ 이제부터 source가 존재할 때  미소 다이폴에 의한  전자기 파동방정식을 유도해 보자.
이 방정식은 vector potential에 의해서 결정된다. 먼저, 자계 static vector potential을 구해보자.

윗 그림으로부터 Biot-Savart' law을 이용해서  전류 밀도  가 있을 때 자기장을 유도해 보자.
 

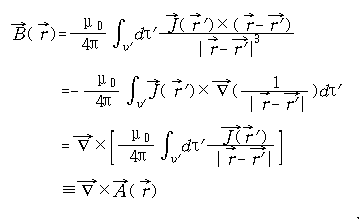
여기서, magnetic vector potential    을 얻는다.
즉, 이것은 vector poisson equation  의 해가 된다.
지금까지 static vector potential을 구했다.
이제부터는 maxwell equation을 이용해서 dynamic vector potential 이 만족하는 equation을 구해보자.
암페어의 법칙으로부터  모드해 을 가정하면,
  

얻는다.
Faraday's law 으로부터  모드해  를 가정하면, 얻는다.
비안키 항등식  으로부터   라 할 수 있고, 여기서
가 된다. 이것을 윗 식에 대입하면

여기서  인 게이지를 선택할 수 있다.
그러면, 을 얻는다.  
이것으로부터 세 개의 scalar Helmholtz 방정식을 얻는다.

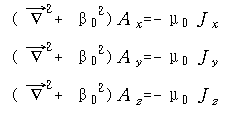
이것의 해는 다음과 같이 주어진다.

다음으로 Ampere's law 으로부터  , 와  에 관한 다음 관계식을 얻는다.

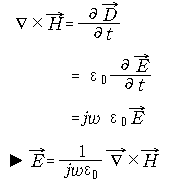
④ 이제부터 미소다이폴  안테나에 의한 자계의 세기  와 전계의 세기 를 구하려고 한다.

 미소 다이폴에 의한 vector potential을 구하면

다음  이므로 먼저  를 구하자.
미소 다이폴 configaration 은 구면좌표계  표현하는 것이 쉽다.

  따라서 직각 좌표계로 표시된  vector potential 인 ""를 구좌표 성분으로 다음과 같이 표시한다.
 

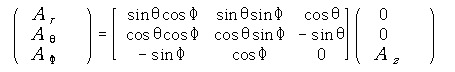
이것으로 부터

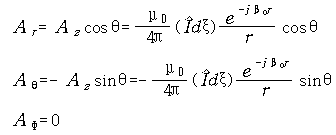
을 얻었다.

      

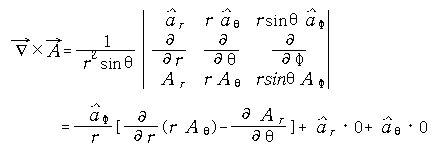
에서 자계의 세기  를 구하면 아래와 같다.

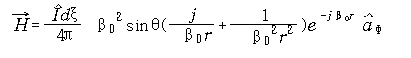
이제부터는 전계의 세기 ( )를 구해보자.
  을 구해보자.

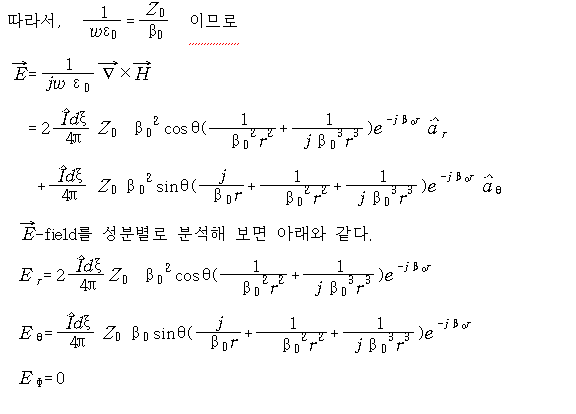
r 이 아주 멀리 떨어져 있을 경우는    항 만 살아남게 된다.

 따라서,

얻는다.